Найдите площадь параллелограмма, изображённого на рисунке
Задача:
Найдите площадь параллелограмма, изображённого на рисунке.
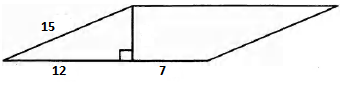

Задача:
Найдите площадь параллелограмма, изображённого на рисунке.

Найдите площадь параллелограмма, изображенного на рисунке.
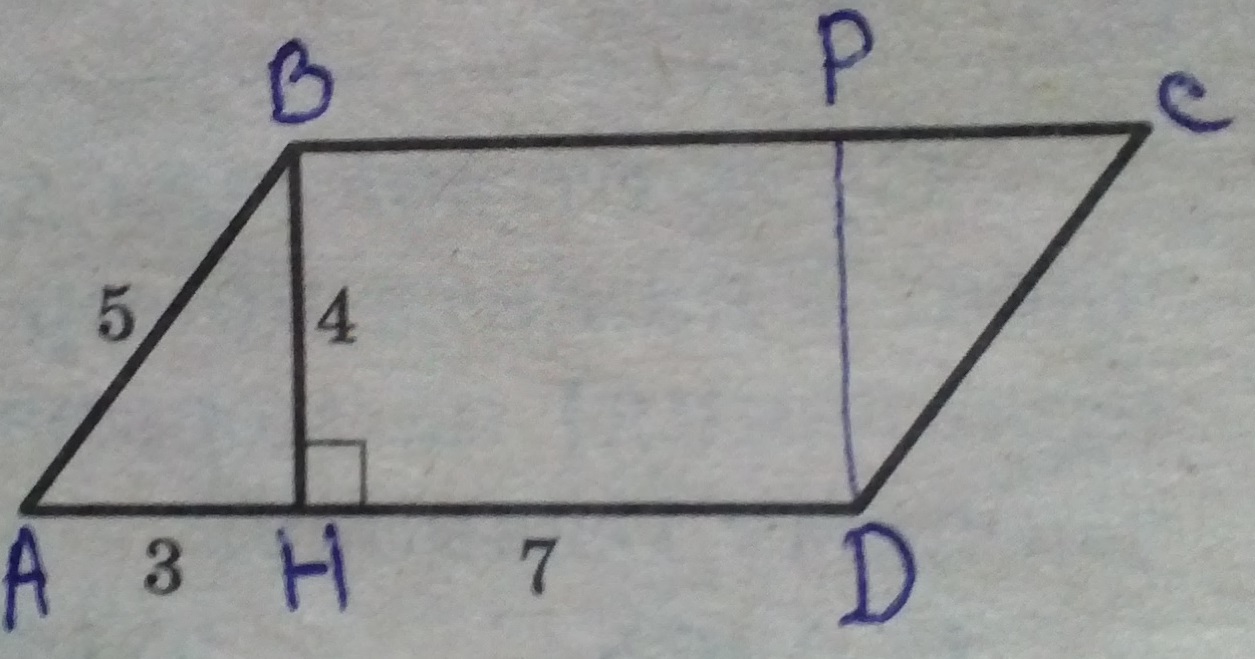
Решение:
Посмотрим на рисунок и назовем параллелограмм ABCD, в котором BH – высота. Проведем еще одну высоту PD. Как видим, получили два одинаковых, в которых AH = PC = 3, AB = CD = 5, BH = PD = 4. Также мы получили прямоугольник BPDH, BH параллельно PD ⇒ BH = PD = 4, BP параллельно HD ⇒ BP = HD = 7.
Чтобы найти S abcd, найдем площади двух треугольников и прямоугольника.
S BPDH = a * b
S BPDH = 4 * 7
S BPDH = 28
Площадь прямоугольного треугольника находится по формуле: S = ½ a* b, где a, b – катеты.
S ABH = ½ * 3 * 4
S ABH = 6
Треуг ABH = треуг PCD
S ABCD = S ABH + S BPDH + S PCD
S ABCD = 6 + 28 + 6
S ABCD =40.
Ответ: 40