Дан куб ABCDA1B1C1D1. Объём треугольной пирамиды A1BC1D равен 3
Задача:
Дан куб ABCDA1B1C1D1. Объём треугольной пирамиды A1BC1D равен 3. Чему равен объём куба?


Задача:
Дан куб ABCDA1B1C1D1. Объём треугольной пирамиды A1BC1D равен 3. Чему равен объём куба?

Задача:
Цилиндр и конус имеют общее основание и высоту. Объём цилиндра равен 120. Найдите объём конуса.

Задача:
Найдите объём правильной шестиугольной призмы, стороны основания которой равны 2√2, а боковые рёбра равны 6√3
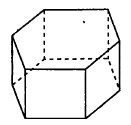
Задача.
Цилиндр и конус имеют общее основание и общую высоту. Вычислите объем цилиндра, если объем конуса равен 17.
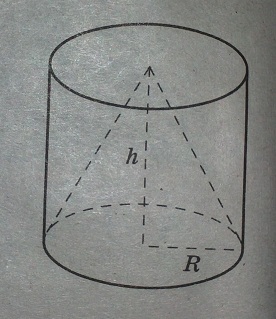
Решение:
Запишем формулу для поиска объемов конуса и цилиндра:
Vк = 1/3 Sосн * h
Vц = Sосн * h
Заметим, что в этой задаче основание и высота конуса и цилиндра совпадают.
Объем конуса равен 17, значит, 1/3 Sосн * h = 17. Отсюда выразим Sосн * h = 17 * 3 = 51 - это и будет выражение справа в формуле Vц = Sосн * h .
Ответ: 51.
Задача.
Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в 6 раз?
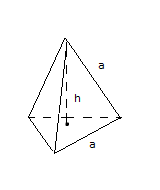
Решение:
Правильный тетраэдр - это треугольная пирамида ,у которой все рёбра равны.
Обозначим длину ребра исходной пирамиды за а, тогда длина ребра второй пирамиды будет равна 6а.
Напомним формулу для поиска объема пирамиды: V = 1/3 Sосн * h (где Sосн - площадь основания, а h - высота, опущенная к этому основанию).
Найдем V1 - объем исходной пирамиды и V2 - объем увеличенной пирамиды.
В основании лежит равносторонний треугольник со стороной а. По формуле поиска площади треугольника S = 1/2a * b * sina имеем:
S1 = 1/2 * a * a * sin60 = 1/2a2 * √3/2 = √3/4 * a2 - площадь основания первой пирамиды
S2 = 1/2 * 6a * 6a * sin60 = 1/2 * 36a2 * √3/2 = √3/4 * 36a2 - площадь основания второй пирамиды.
Заметим, что если увеличили все ребра в 6 раз, то и высота увеличилась в 6 раз. Значит, h2 = 6h1.
Нам нужно найти V2 / V1 =
(1/3 Sосн2 * h2) / (1/3 Sосн1 * h1) =
(1/3 * √3/4 * 36a2 * 6h1) / (1/3 * √3/4 * a2 * h1) = 36*6 = 216 (так как все остальное сократилось).
Ответ: 216.
Ещё статьи...