В равнобедренной трапеции сумма углов, прилежащих к большему основанию, равна

В равнобедренной трапеции сумма углов, прилежащих к большему основанию, равна 98

Задача:

В равнобедренной трапеции сумма углов, прилежащих к большему основанию, равна 98°. Найдите величину тупого угла трапеции.

Подробнее...

Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33

Задача:

Сторона треугольника равна 12, а высота, проведённая к этой стороне, равна 33. Найдите площадь треугольника.

Подробнее...

Найдите площадь прямоугольного треугольника, если один из его катетов равен 12 см, а гипотенуза равна 13 см.

Найдите площадь прямоугольного треугольника, если один из его катетов равен 12 см, а гипотенуза равна 13 см.

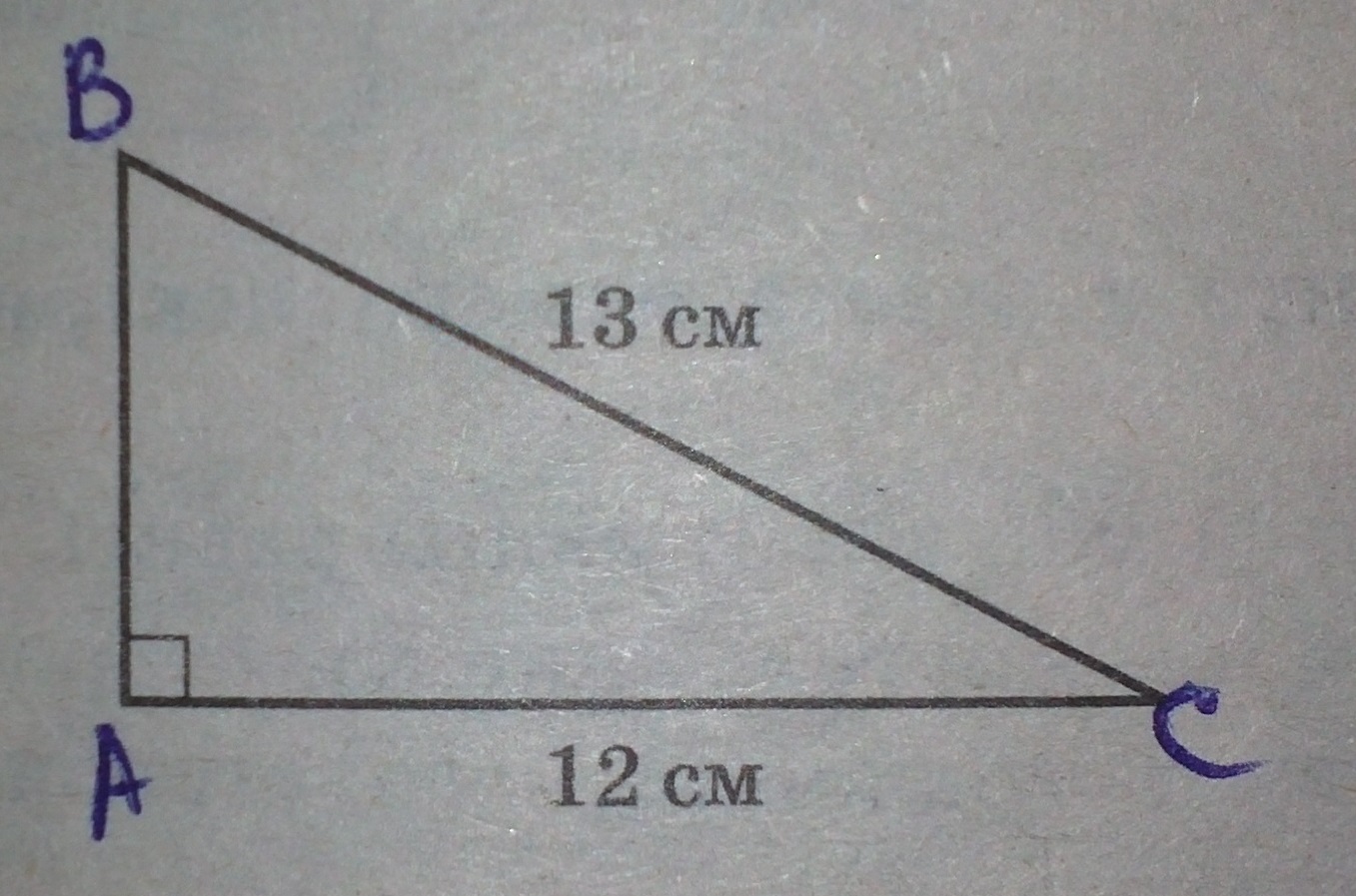
Решение:

Обозначим буквами и получим треугольник АВС. АС (катет)= 12, ВС (гипотенуза)= 13, Найдем АВ по Теореме Пифагора:

АС² = АВ² + ВС²

122 = АВ² + 13²

144 = АВ² + 169

АВ² = 169 - 144

АВ² = 25

АВ = ± √ 25 = ± 5, -5 не имеет значения в данной задаче, ⇒ АВ = 5.

S треуг = ½ a * h

В треугольнике АВС а (катет) = 12, h = 5.

S треуг = ½ * 12 * 5 = 30 см² – площадь прямоугольного треугольника.

Ответ: 30.

В треугольнике ABC стороны AB и BC равны, а внешний угол при вершине С равен 123 градуса. Найдите величину угла B.

В треугольнике ABC стороны AB и BC равны, а внешний угол при вершине С равен 123 градуса. Найдите величину угла B.

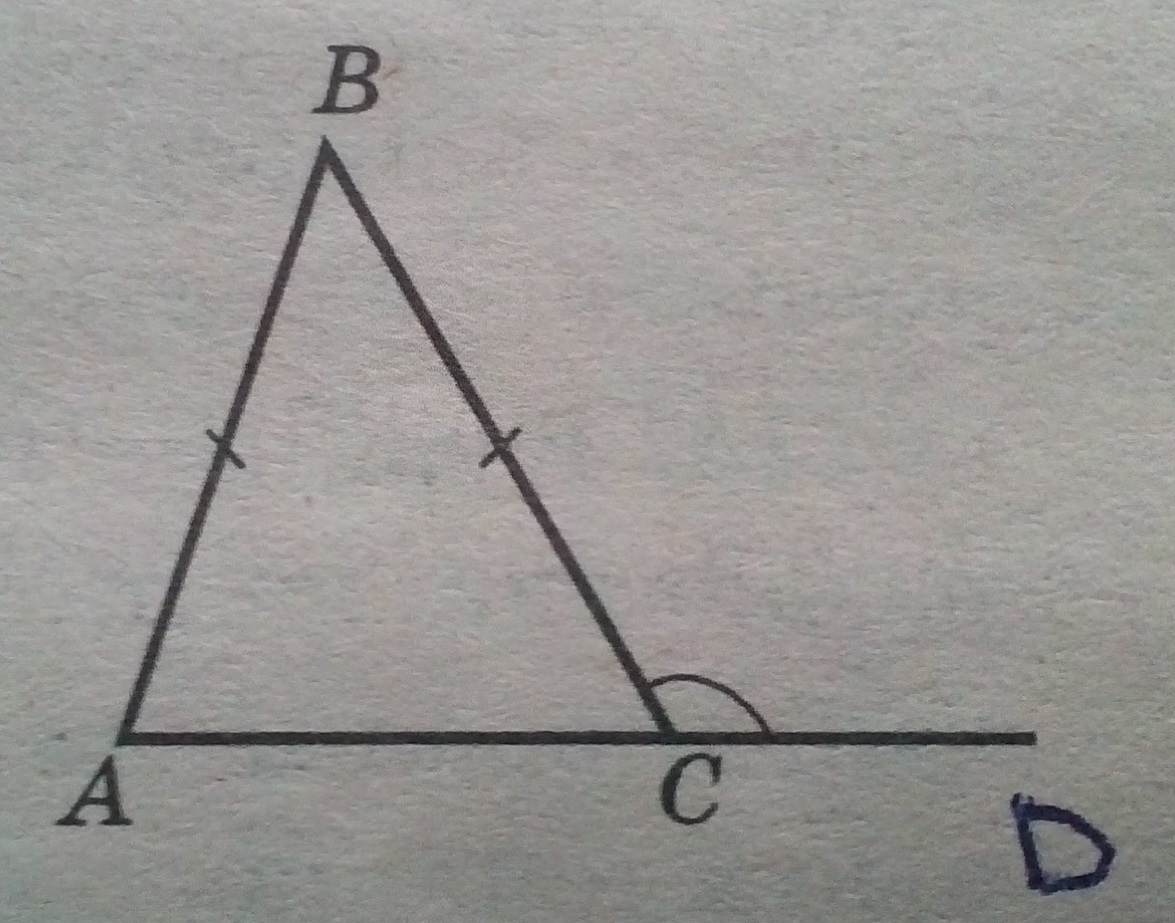
Решение:

Посмотрим на условие, AB = BC, значит треугольник равнобедренный, а в равнобедренном треугольнике углы при основании равны,⇒ угол A = углу C.

ACD – развернутый угол, который равен 180°. BCD по условию = 123 градуса, найдем угол С:

180° – 123° = 57°

Так как С = 57, то и А = 57, так как они равны.

Мы знаем, что сумма углов любого треугольника равна 180 градусов. Найдем из этого правила угол В:

∠A + ∠B + ∠C = 180°

57° + ∠В + 57° = 180°

114° + ∠В = 180°

∠В = 180° – 114°

Угол В = 66°

Ответ: 66.