Цилиндр, объём которого равен 66, описан около шара. Найдите объём шара
Задача: Цилиндр, объём которого равен 66, описан около шара. Найдите объём шара
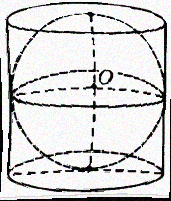
Решение:
По рисунку мы видим, что диаметр шара - это диаметр окружности основания цилиндра и при этом является высотой цилиндра.
Пусть радиус шара равен R, значит его D=2R, значит, высота цилиндра H равна 2R. Находим объём цилиндра: Vцил. = Sосн. * H = πR2 * 2R = 2πR3.
По условию 66 = 2πR3.
πR3 = 33.
Так как Vшара = 4/3 *πR3, то объём равен 4/3 * 33 = 44.
Ответ:44