Найдите площадь прямоугольного треугольника, если один из его катетов равен 12 см, а гипотенуза равна 13 см.

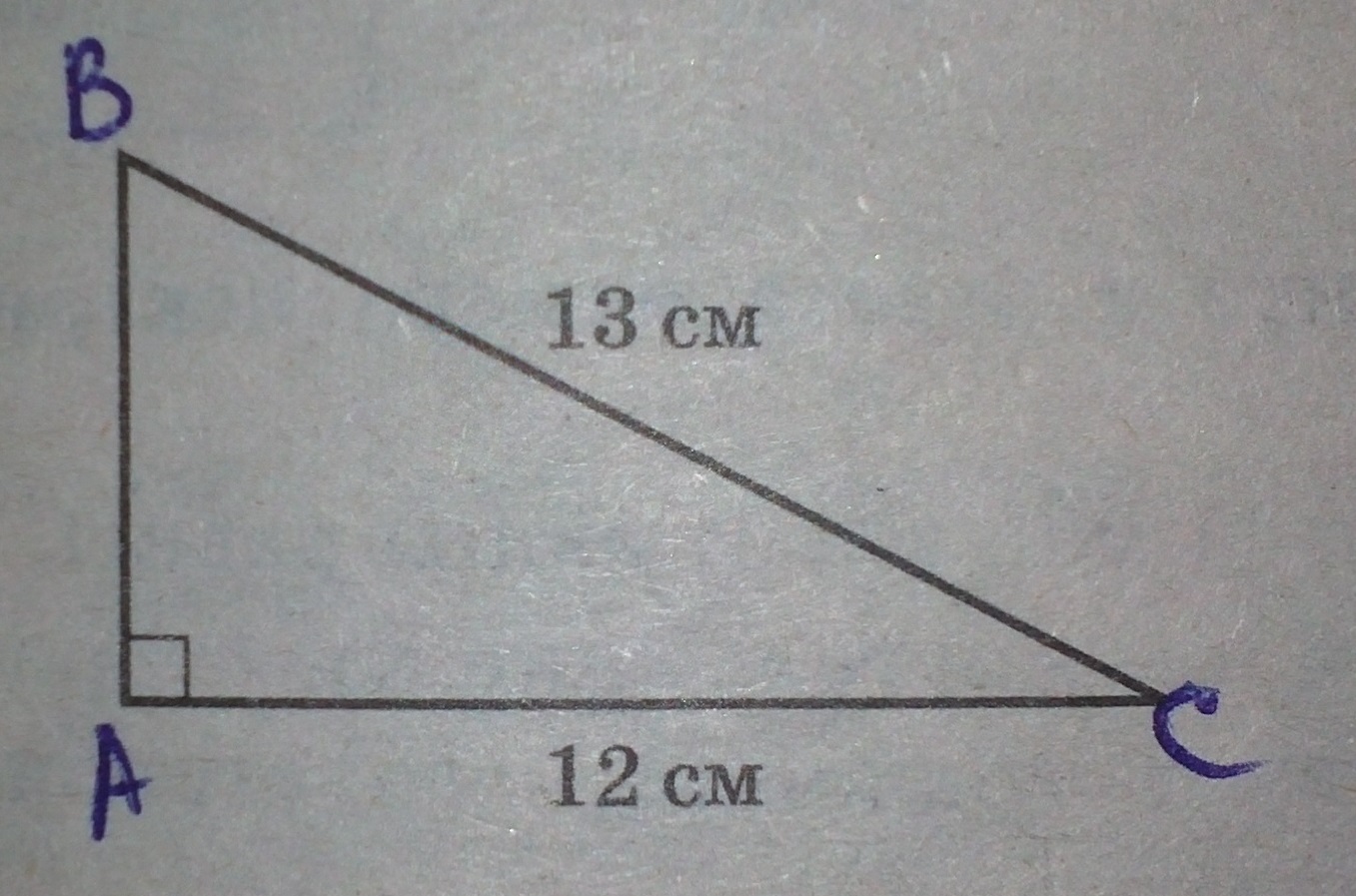
Решение:

Обозначим буквами и получим треугольник АВС. АС (катет)= 12, ВС (гипотенуза)= 13, Найдем АВ по Теореме Пифагора:

АС² = АВ² + ВС²

122 = АВ² + 13²

144 = АВ² + 169

АВ² = 169 - 144

АВ² = 25

АВ = ± √ 25 = ± 5, -5 не имеет значения в данной задаче, ⇒ АВ = 5.

S треуг = ½ a * h

В треугольнике АВС а (катет) = 12, h = 5.

S треуг = ½ * 12 * 5 = 30 см² – площадь прямоугольного треугольника.

Ответ: 30.