03. В14. Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 3,5 км от места отправления. Один идет со скоростью 2,7 км/ч, а другой - со скоростью 3,6 км/ч. Дойдя до опушки, второй с той же скоростью возвращается
Задача.
Два человека отправляются из одного и того же места на прогулку до опушки леса, находящейся в 3,5 км от места отправления. Один идет со скоростью 2,7 км/ч, а другой - со скоростью 3,6 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдет их встреча?
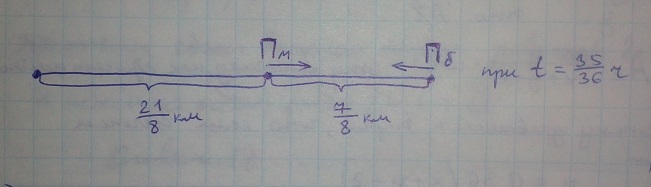
Картинка в момент времени t = 35/36 ч, когда "быстрый" пешеход развернулся и пошел навстречу "медленному".
Решение:
Найдем вначале время, за которое второй человек (кто шел быстрее) дошел до опушки. Из формулы S = V * t имеем: t = S/V = 3,5 : 3,6 = 35/36 ч.
А первый "медленный" за это время прошел путь S = V * t = 2,7 * 35/36 = 21/8 км.
Это значит, что расстояние (3,5 - 21/8) = 7/8 км они двигались навстречу друг другу с общей скоростью (2,7 + 3,6) = 6,3 км/ч.
Найдем время, через которое они встретились с момента, когда "быстрый" человек развернулся: 7/8 : 6,3 = 5/36 ч.
Значит, "медленный" человек, пройдя 21/8 км еще шел 5/36 часа до встречи. Найдем это расстояние: S = V * t = 2,7 * 5/36 = 3/8 км.
И сложим первую часть пути "медленного" человека 21/8 км со второй частью его пути 3/8 км: 21/8 + 3/8 = 24/8 = 3 км.
Ответ: 3.

