12. В5. Найдите площадь четырехугольника, вершины которого имеют координаты (2; 6), (2; 9), (8; 5), (8; 2).
Задача.
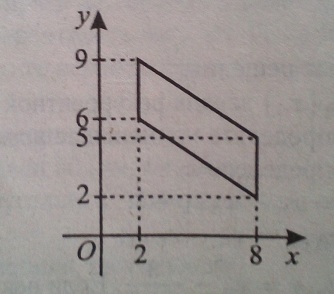
Найдите площадь четырехугольника, вершины которого имеют координаты (2; 6), (2; 9), (8; 5), (8; 2).
Решение:
Обозначим вершину с координатами (2; 6) за A, вершину (8; 2) за B, вершину (8; 5) за C, вершину (2; 9) за D.
Стороны AD и BC параллельны и равны 9-6=5-2=3 - видно из рисунка, а высота параллелограмма - это расстояние между прямыми AD и BC, равна 8-2=6.
Значит, по формуле для поиска площади параллелограмма получим: S=AD*h, где h - высота, проведенная к AD. Поэтому S=3*6=18.
Ответ: 18.

