07. В5. Площадь параллелограмма ABCD равна 6. Найдите площадь параллелограмма A'B'C'D'...
Задача.
Площадь параллелограмма ABCD равна 6. Найдите площадь параллелограмма A'B'C'D', вершинами которого являются середины сторон данного параллелограмма.
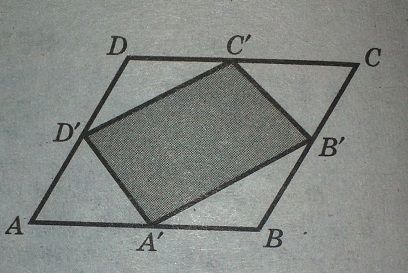
Решение:
Решим задачу двумя способами.
1 способ:
Так как D′ и B′ - середины сторон, то отрезок D′B′ разделит параллелограмм пополам, тогда площадь параллелограмма D′DCB′ будет равна половине площади ABCD, то есть 1/2*6=3.
Заметим, что у параллелограмма D′DCB′ и треугольника D′C′B′ совпадает основание D′B′ и высота h, проведенная из вершины C′ на сторону D′B′.
Поэтому площадь параллелограмма D′DCB′ будет равна (из формулы S=b*h) : D′B′*h=3, а площадь треугольника D′C′B′ равна ½D′B′*h=3/2 (из формулы S=½b*h, где в обеих формулах b - сторона треугольника, а h - высота, проведенная к этому основанию).
И так как видно, что площадь искомого параллелограмма равна сумме двух площадей треугольников D′C′B′ и D′B′A′, которые равны 3/2. Значит, 3/2+3/2=3.
Ответ: 3.
2 способ:
По формулам S=a*b*sinα и S=½D1D2*sinβ, где а, b - стороны параллелограмма, D1D2 - диагонали, α - угол между его сторонами, а β - угол между его диагоналями.
Значит, площадь ABCD по первой формуле равна: AD*AB*sinα=6.
А так как D′B′=АВ, а A'C'=D1D2 , то D′B′*A'C'*sinα=6.
Но заметим, что угол А между AD и AB равен углу между диагоналями D′B′ и A'C'.
Поэтому, площадь искомого параллелограмма равна ½D′B′*A'C'*sinα= ½*6=3 (из второй формулы).
Ответ: 3.

