01. В8. На окружности отмечены точки А, В и С. Дуга окружности АС, не содержащая точку В, составляет 130 градусов. Дуга окружности ВС, не содержащая точку А, составляет 72 градуса.
Задача.
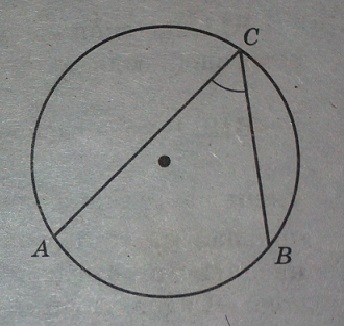
На окружности отмечены точки А, В и С. Дуга окружности АС, не содержащая точку В, составляет 130 градусов. Дуга окружности ВС, не содержащая точку А, составляет 72 градуса. Найдите вписанный угол АСВ. Ответ дайте в градусах.
Решение:
Для решения данного типа задач необходимо знать 2 факта:
1) Полная дуга окружности составляет 360 градусов;
2) Любой вписанный угол в окружности равен половине дуги окружности, на которую этот угол упирается.
Определим, сколько градусов составляет дуга, на которую опирается искомый угол АСВ. Видим по рисунку, что нарисованная окружность разделена на три дуги, две из которых известны, а третью надо определить для решения задачи.
Известны дуги АС, ВС, которые в сумме составляют 130°+72°=202°. Значит, дуга АВ равна 360°-202°=158°.
Используя то, что угол АСВ опирается на эту дугу, составляющую 158 градусов, находим величину нашего угла АСВ: ½*158°=79°.
Ответ: 79.

