08. В9. На рисунке изображен график функции y=f(x) и касательная к этому графику, проведенная в точке с абсциссой Х0. Найдите значение производной функции f(x) в точке Х0.
Задача.
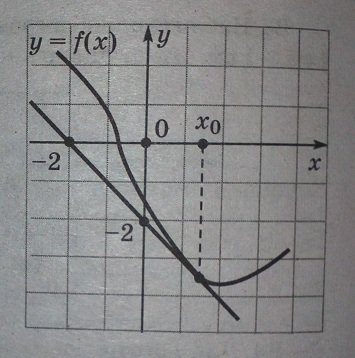
На рисунке изображен график функции y=f(x) и касательная к этому графику, проведенная в точке с абсциссой Х0. Найдите значение производной функции f(x) в точке Х0.
Решение:
Мы должны знать, что производная функции f(x) в точке х0 равна коэффициенту K при х в уравнении прямой, касательной к f(x) в точке х0.
То есть, если нам надо найти f´(x0), то мы просто найдем K в уравнении прямой y = Kx + b.
Из графика видно, что наша касательная проходит через точки (-2; 0) и (0; -2). Подставим их в уравнение прямой: х1 = -2, у1 = 0 и х2 = 0, у2 = -2 и получим 2 уравнения:
1) 0 = K(-2) + b
2) -2 = K * 0 + b
Это система двух уравнений, найдем из нее K.
Из (2) b = -2 подставим в (1):
0 = -2K - 2
K = -2/2
K = -1.
-1 - искомое значение f´(x0).
Ответ: -1

