В треугольнике АВС АС=ВС=12, tgA=корень(2)/4. Найдите высоту СН.
Задача: В треугольнике АВС АС=ВС=12, tgA=кв.корень(2)/4. Найдите высоту СН.
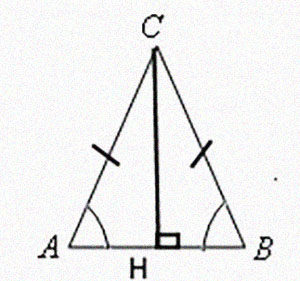
Решение:
tgA=СН/АН=√2/4
Пусть СН=√2x, то AH=4x.
По теореме Пифагора из треугольника АСН:
(АН)2+(СН)2=(АС)2
16x2+2x2=144
x2=144:18
x=2√2
Получается, СН=√2·2√2=4
Ответ: 4

