09. В6. Пенсионер гуляет по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Пенсионер начинает прогулку в точке А. Найдите вероятность того, что он придет в точку G.

Задача.

Пенсионер гуляет по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показана на рисунке. Пенсионер начинает прогулку в точке А. Найдите вероятность того, что он придет в точку G.

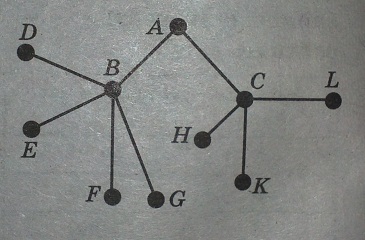
Решение:

Чтобы попасть в точку G, пенсионер должен будет сначала попасть в точку В (так как если он сначала попадет в точку С, то по условию задачи вернуться обратно в точку A он не сможет).

Поэтому нам нужно знать, что такое условная вероятность.

6) Условная вероятность: Пусть А и В - зависимые события. Условной вероятностью РА(В) события В называется вероятность события В, найденная в предположении, что событие А уже наступило.

Пусть из точки A в точку G должно произойти два события:

Событие М - что пенсионер идет из точки A в точку В.

Событие N - что пенсионер идет из точки В в точку G.

Обозначим за Q событие, что пенсионер попадет в точку G по формуле Р(Q) = Р(М) * Рм(N).

Найдем Р(М) = 1/2 по определению вероятности

Найдем Рм(N) = 1/4 тоже по определению вероятности.

1) Вероятность события А - это отношение числа исходов, благоприятствующих его наступлению к числу всех исходов (несовместных, единственно возможных и равновозможных). Р(А)= m/n, где m - число благоприятных исходов, а n - число всех исходов.

Поэтому Р(Q) = 1/2 * 1/4 = 1/8 = 0,125 (по формуле поиска вероятности произведения событий : 7) Теорема: Вероятность произведения двух зависимых событий А и В равна произведению вероятности одного из них на условную вероятность другого, найденного в предположении, что первое событие уже наступило: Р(А*В) = Р(А) * РА(В).)

Ответ: 0,125.

Подобные задачи: http://dnevnikanet.ru/b10-resheniya

http://dnevnikanet.ru/b10-resheniya/1