08. В10. В правильной треугольной пирамиде SABC ребра BA и BC разделены точками K и L так, что BK=BL=4 и KA=LC=2. Найдите угол между плоскостью основания ABC и плоскостью сечения SKL. Ответ выразите в градусах.
Задача.
В правильной треугольной пирамиде SABC ребра BA и BC разделены точками K и L так, что BK=BL=4 и KA=LC=2. Найдите угол между плоскостью основания ABC и плоскостью сечения SKL. Ответ выразите в градусах.
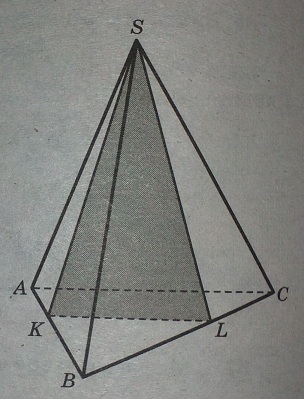
Решение:
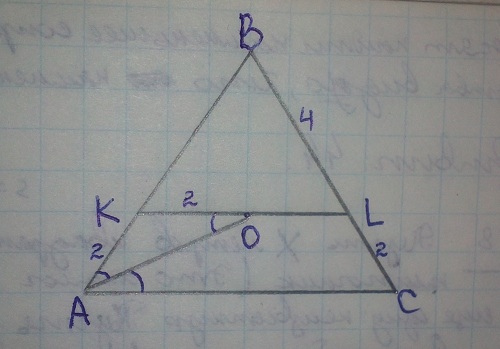
По определению правильной треугольной пирамиды ее основание треугольник ABC - это правильный (то есть равносторонний) треугольник.
Заметим, что треугольник KBL тоже равносторонний (так как он подобен ABC), значит, KL=KB=4.
Рассмотрим точку О - середину отрезка KL. Тогда KO = 2.
Значит, треугольник AKO равнобедренный, так как AK = 2 по условию задачи.
Значит, угол KAO = углу KOA (как углы при основании равнобедренного треугольника)
Заметим еще, что угол KOA = углу OAC (как накрест лежащие углы)
Поэтому доказано, что AO - биссектриса треугольника ABC. Аналогично CO - биссектриса треугольника ABC. Значит, точка О - центр треугольника ABC.
В правильной треугольной пирамиде высота SO будет соединять вершину S с точкой О - центром равностороннего треугольника.
Тем самым мы доказали, что SO - высота пирамиды.
И так как плоскость SKL содержит SO - прямую, перпендикулярную плоскости ABC, то эти две плоскости перпендикулярны. Значит, угол между ними равен 90°.
Ответ: 90.

