06. В8. В треугольнике АВС АС=ВС=12, sinВ = корень из 15/4. Найдите АВ.
Задача.
В треугольнике АВС АС=ВС=12, sinВ = корень из 15/4. Найдите АВ.
Решение:
Вначале нарисуем сам треугольник АВС и посмотрим на него. Он равнобедренный со сторонами АС=ВС=12.
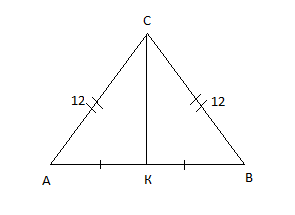
Проведем высоту СК - перпендикуляр из точки С на сторону АВ.
Так как синус угла В в прямоугольном треугольнике КСВ - это отношение противолежащего катета к гипотенузе СВ, то это равно:
СК/СВ= √15/4, откуда имеем СК/12=√15/4. Значит, СК равно 3√15.
Высота СК делит сторону АВ пополам, так как треугольник АВС равнобедренный. Таким образом, АК=КВ. Значит, АВ=АК+КВ=2КВ.
Теперь найдем сторону КВ из прямоугольного треугольника КСВ по теореме Пифагора:
СК2+КВ2=СВ2, подставим СК=3√15 и СВ=12 и получим:
(3√15)2+КВ2=122
КВ2=144-135
КВ2=9
КВ=√9
КВ=3
Отсюда получим АВ=2КВ=2*3=6.
Ответ: 6.

