07. В8. В треугольнике АВС АС=ВС=5, АВ=8. Найдите tgА.

Задача.

В треугольнике АВС АС=ВС=5, АВ=8. Найдите tgА.

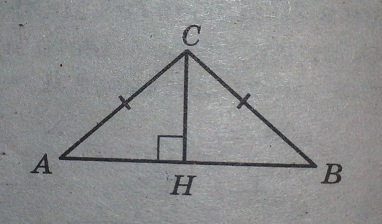
Решение:

Рассмотрим прямоугольный треугольник АСН.

Определение: Тангенс (tg) угла прямоугольного треугольника равен отношению противолежащего катета к прилежащему.

Значит, tgА=СН/АН. Найдем СН и АН.

Так как треугольник АВС равнобедренный, то его высота СН делит основание АВ пополам, то есть АН= 8:2=4.
По Теореме Пифагора из треугольника АСН найдем СН:

АС²=СН²+АН²

5²=СН²=4²

СН²=25-16

СН²=9

СН=√9

СН=3.

Отсюда имеем: tgА=СН/АН=3/4=0,75.

Ответ: 0,75.