01. В9. На рисунке изображен график функции y=f(x), определенной на интервале (-1; 13). Определите количество целых точек, в которых производная функции положительна.
Задача.
На рисунке изображен график функции y=f(x), определенной на интервале (-1; 13). Определите количество целых точек, в которых производная функции положительна.
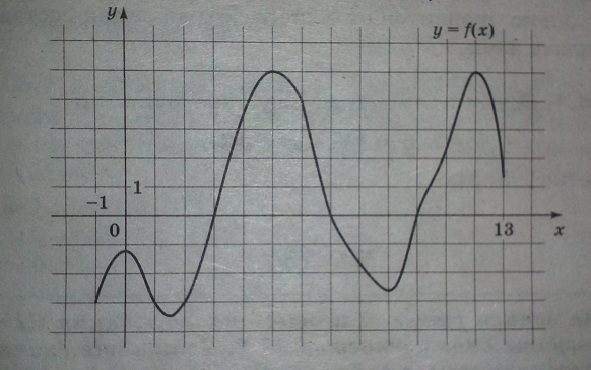
Решение:
Нас просят найти количество таких целочисленных значений х на интервале (-1; 13), в которых функция f(x) возрастает (так как именно в этих точках производная положительна).
Всего целых точек на интервале (-1; 13) 13 штук, это: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, краевые точки не берем, так как нам дан интервал, а не отрезок.
Рассмотрим все 13 точек. При:
х=0: f(x) не убывает и не возрастает, поэтому f′(x) = 0, не подходит.
х=1: f(x) убывает, значит f′(x) < 0, не подходит.
х=2: f(x) возрастает, значит f′(x) > 0, подходящая целая точка.
х=3: f(x) возрастает, значит f′(x) > 0, подходящая целая точка.
х=4: f(x) возрастает, значит f′(x) > 0, подходящая целая точка.
х=5: f(x) не убывает и не возрастает, поэтому f′(x) = 0, не подходит.
х=6: f(x) убывает, значит f′(x) < 0, не подходит.
х=7: f(x) убывает, значит f′(x) < 0, не подходит.
х=8: f(x) убывает, значит f′(x) < 0, не подходит.
х=9: f(x) не убывает и не возрастает, поэтому f′(x) = 0, не подходит.
х=10: f(x) возрастает, значит f′(x) > 0, подходящая целая точка.
х=11: f(x) возрастает, значит f′(x) > 0, подходящая целая точка.
х=12: f(x) не убывает и не возрастает, поэтому f′(x) = 0, не подходит.
Итого имеем пять целых точек, в которых производная положительна, это 2, 3, 4, 10, 11.
Ответ: 5.

