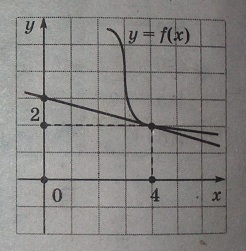
02. В9. На рисунке изображен график функции y=f(x) и касательная к этому графику, проведенная в точке с абсциссой 4. Найдите значение производной функции y=f(x) в точке Х0=4.
Задача.
На рисунке изображен график функции y=f(x) и касательная к этому графику, проведенная в точке с абсциссой 4. Найдите значение производной функции y=f(x) в точке Х0=4.
Решение:
У подобных задач есть несколько способов решения. Решим задачу одним из них. Требуется найти f′(x) - значение производной функции f(x) в точке х0.
Вспомним, что f′(x) равно коэффициенту k уравнения касательной в точке х0 к графику функции f(x). На рисунке эта касательная показана и нетрудно будет найти уравнение этой прямой.
Уравнение любой прямой может быть записано в виде y = kx + b. Из рисунка видно, что наша прямая проходит через точки х1 = 0, у1 = 3 и х0 = 4, у0 = 2.
Подставим сначала в общее уравнение прямой х1 = 0, у1 = 3 и получим: 3 = k*0 + b. Отсюда имеем b = 3.
Подставим теперь в общее уравнение прямой х0 = 4, у0 = 2, b = 3 и получим: 2 = k*4 + 3, отсюда найдем k = -1/4 = -0,25 - это у нас и будет f′(x0).
Ответ: -0,25.

