07. В13. В правильной треугольной пирамиде SABCD N - середина ребра BC, S - вершина. Известно, что SN= 6, а площадь боковой поверхности равна 72. Найдите длину отрезка AB.

Задача.

В правильной треугольной пирамиде SABCD N - середина ребра BC, S - вершина. Известно, что SN= 6, а площадь боковой поверхности равна 72. Найдите длину отрезка AB.

В правильной треугольной пирамиде SABCD N - середина ребра BC, S - вершина. Известно, что SN= 6, а площадь боковой поверхности равна 72. Найдите длину отрезка AB.

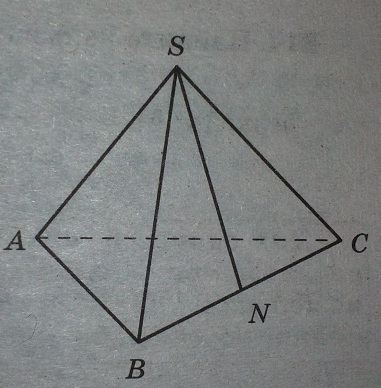
Решение:

Так как пирамида правильная, то ее грани равны и их площади равны. Обозначим за F площадь одной боковой грани (например, BSC). Из того, что площадь боковой поверхности равна 72, то имеем: F+F+F = 72 ⇔ 3F = 72 ⇔ F = 24, то есть площадь треугольника BSC равна 24.

Так как треугольник BSC равнобедренный, то его медиана SN будет еще и высотой. По формуле F = 1/2 a*h для поиска площади треугольника имеем:

24 = 1/2 * BC * SN ⇔

24 = 1/2 * BC * 6 ⇔

24 = 3 * BC ⇔ 

BC = 8. И так как в основании  правильной треугольной пирамиды правильный треугольник, то и AB=BC=8.

Ответ: 8.