04. В13. В правильной треугольной пирамиде SABCD M - середина ребра AB, S - вершина. Известно, что BC=4, а площадь боковой поверхности пирамиды равна 18. Найдите длину отрезка SM.

Задача.

В правильной треугольной пирамиде SABCD M - середина ребра AB, S - вершина. Известно, что BC=4, а площадь боковой поверхности пирамиды равна 18. Найдите длину отрезка SM.

В правильной треугольной пирамиде SABCD M - середина ребра AB, S - вершина. Известно, что BC=4, а площадь боковой поверхности пирамиды равна 18. Найдите длину отрезка SM.

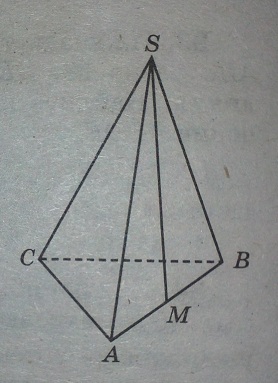
Решение:

Так как пирамида правильная, то треугольник в основании ABC равносторонний, ⇒ AB=BC=CA=4. И боковые ребра тоже равны: SA=SB=SC.

То есть боковая поверхность пирамиды состоит из трех равных равнобедренных треугольников SAB, SBC, SCA; а площадь боковой поверхности равна сумме площадей этих треугольников, которые равны между собой. Поэтому площадь треугольника SAB равна 18:3=6.

С другой стороны заметим, что в этом равнобедренном треугольнике SAB есть медиана SM, которая еще и является высотой, поэтому площадь треугольника SAB равна: 6=½*AB*SM = ½*4*SM = 2SM ⇒ SM = 6/2 = 3.

Ответ: 3.