08. В8. В треугольнике АВС АВ=ВС, АС=5, cosС=0,8. Найдите высоту СН.

Задача.

В треугольнике АВС АВ=ВС, АС=5, cosС=0,8. Найдите высоту СН.

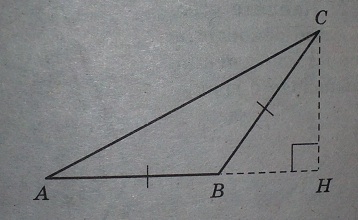
Решение:

Заметим.ю что угол А равен углу С, так как треугольник АВС равнобедренный. Значит, cosС = cosА = 0,8.

Из прямоугольного треугольника АСН имеем: cosА=АН/АС - отношение прилежащего катета к гипотенузе. Подставим известные нам значения в выражение и получим: 0,8=АН/5. Отсюда получим АН=0,8*5=4.

По теореме Пифагора из треугольника АСН имеем:

АС²=АН²+СН²

5²=4²+СН²

СН²=25-16

СН²=9

СН=√9

СН=3.

Ответ: 3.