03. В9. На рисунке изображен график первообразной y=F(x) некоторой функции y=f(x), определенной на интервале (-16; -2)...
Задача.
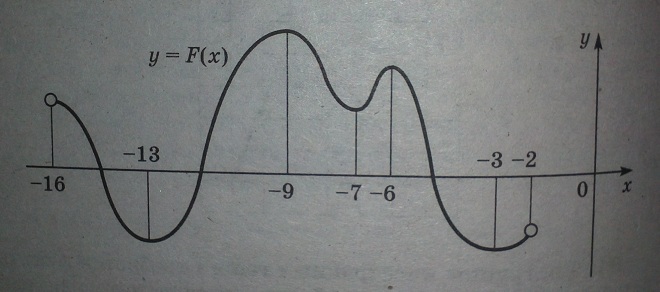
На рисунке изображен график первообразной y=F(x) некоторой функции y=f(x), определенной на интервале (-16; -2). Пользуясь рисунком, определите количество решений уравнения f(x)=0 на отрезке [-14;-8].
Решение:
По определению первообразной имеем F′(x) = f(x).
Нас просят найти количество точек, в которых f(x) = 0, то есть F′(x) = 0.
На рисунке изображен график функции у = F(x). Производная этой функции F′(x) равна нулю в точках максимума и минимума.
На отрезке [-14; -8] таких точек всего две - это х1 = -13 - точка минимума и х2 = -9 - точка максимума.
Поэтому F′(x) равно нулю в этих точках на отрезке [-14; -8].
Значит, количество решений уравнения f(x) = 0 или что тоже самое F′(x) = 0 будет иметь 2 решения.
Ответ: 2.

