04. В9. На рисунке изображен график некоторой функции y=f(x). Одна из первообразных этой функции равна F(x)= (-1/3)x в степени 3 -(7/2)х в степени 2 -10х -6. Найдите площадь закрашенной фигуры.
Задача.
На рисунке изображен график некоторой функции y = f(x). Одна из первообразных этой функции равна F(x)= (-1/3x3) - (7/2)х2 - 10х - 6. Найдите площадь закрашенной фигуры.
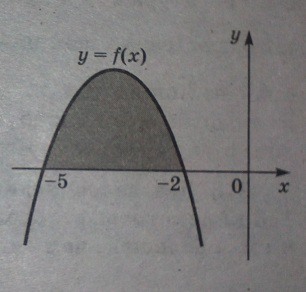
Решение:
Площадь фигуры, ограниченной графиком функции y = f(x) на отрезке [-5; 2] равна:
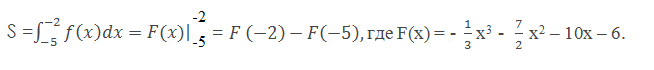
Найдем сначала F (-2) : -1/3 * (-2)3 - 7/2 * (-2)2 - 10 * (-2) - 6 = 8/3 - 14 + 20 - 6 = 8/3.
Теперь найдем F (-5) : -1/3 * (-5)3 - 7/2 * (-5)2 - 10 * (-5) - 6 = 125/3 - 7/2*25 + 50 - 6 = 125/3 - 87,5 + 44 = 125/3 - 43,5.
И найдем F (-2) - F (-5) : 8/3 - (125/3 - 43,5) = 8/3 - 125/3 + 43,5 = 4,5 - это и есть искомая площадь фигуры.
Ответ: 4,5.

