10. В9. Функция y=f(x) определена на интервале (-3; 5). На рисунке изображен график ее производной. Определите, сколько существует касательных к графику функции y= f(x), которые параллельны прямой y=3x-5 или совпадают с ней.
Задача.
Функция y=f(x) определена на интервале (-3; 5). На рисунке изображен график ее производной. Определите, сколько существует касательных к графику функции y= f(x), которые параллельны прямой y=3x-5 или совпадают с ней.
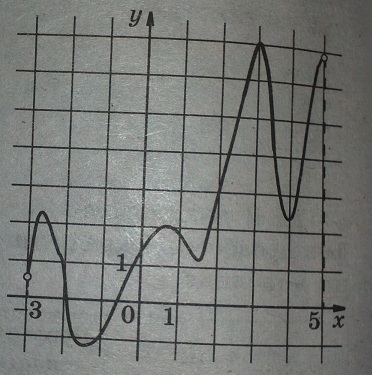
Решение:
Для наглядности нужно нарисовать указанную прямую y= 3x - 5. Найдем для этого две точки, через которые она проходит и проведем через них прямую.
Если х = 2, то у = 3*2 - 5 = 6-5 = 1,
Если х = 3, то у = 3*3 - 5 = 9-5 = 4.
То есть прямая проходит через точки (2;1) и (3;4), проведем через них прямую:
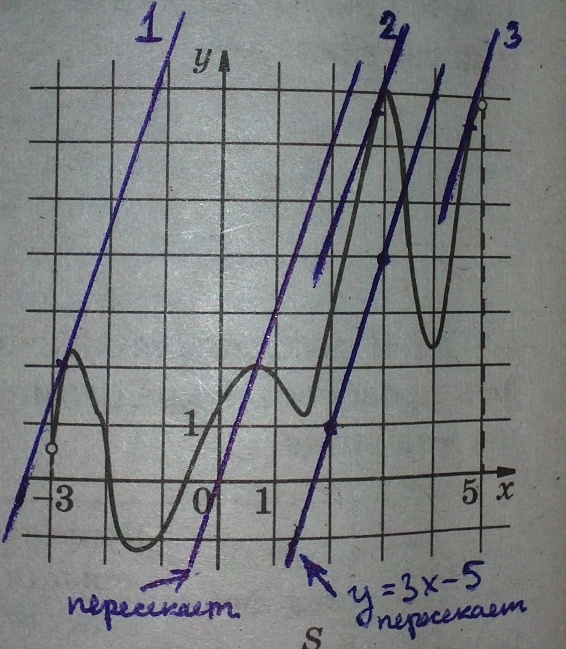
Теперь визуально определим, сколько может быть касательных к нарисованному графику, параллельных нарисованной прямой (очевидно, что сама она не является касательной, поэтому условие "совпадает с ней" нам не подходит).
И из рисунка видно, что таких прямых, параллельных данной и являющихся касательной, всего может быть три, а остальные прямые, параллельные данной, будут пересекать график функции, а не будут касаться.
Ответ: 3.

