04. В5. Площадь треугольника ABC равна 28. DE - средняя линия. Найдите площадь трапеции ABDE.

Задача.

Площадь треугольника ABC равна 28. DE - средняя линия. Найдите площадь трапеции ABDE.

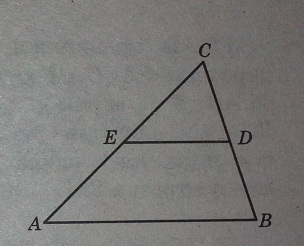
Решение:

По условию задачи площадь треугольника АВС =28. Пусть высота треугольника АВС, опущенная из вершины С на сторону АВ равна h. Тогда по формуле

площадь треугольника АВС будет равна: S=½АВ*h=28,

а площадь трапеции ABDE будет равна: S_тр= ½(AB+ED)*h/2 (высота трапеции равна h/2, так как ED разделит высоту h пополам.

Еще из условия задачи видим, что ED - средняя линия, а это значит: ED=½АВ - по определению средней линии.

Теперь подставим ED=½АВ в формулу площади трапеции и получим:

S_тр= ½(АВ+½АВ)*h/2= 1/2*3/2АВ*h/2= ½АВ*h*¾.

А так как ½АВ*h=28, то подставив, получим: S_тр=28*¾=21.

Ответ: 21.