02. В13. В правильной четырехугольной пирамиде SABCD точка O - центр основания, S - вершина, SC=73, AC=110. Найдите длину отрезка SO.

Задача.

В правильной четырехугольной пирамиде SABCD точка O - центр основания, S - вершина, SC=73, AC=110. Найдите длину отрезка SO.

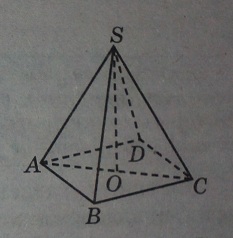
Решение:

Так как пирамида SABCD правильная, то в основании лежит правильный четырехугольник, то есть квадрат. Точка O разделит диагональ квадрата ABCD пополам, поэтому OC = AC/2 = 110/2 = 55.

Так как пирамида правильная, то высота, опущенная из точки S, попадет в центр основания O. Получается, SO - высота. Поэтому треугольник SOC - прямоугольный. И по теореме Пифагора имеем:

SC²=SO²+OC²⇔

73²=SO²+55²

SO²=73²-55²

SO²= 5329 - 3025

SO² = 2304

SO= √2304

SO=48.

Ответ: 48.