06. В9. Функция y=f(x) определена на интервале (-5; 6). На рисунке изображен график функции y=f(x). Найдите среди точек х1, х2, ..., х7 те точки, в которых производная функции f(x) равна нулю. В ответ запишите количество найденных точек.
Задача.
Функция y=f(x) определена на интервале (-5; 6). На рисунке изображен график функции y=f(x). Найдите среди точек х1, х2, ..., х7 те точки, в которых производная функции f(x) равна нулю. В ответ запишите количество найденных точек.
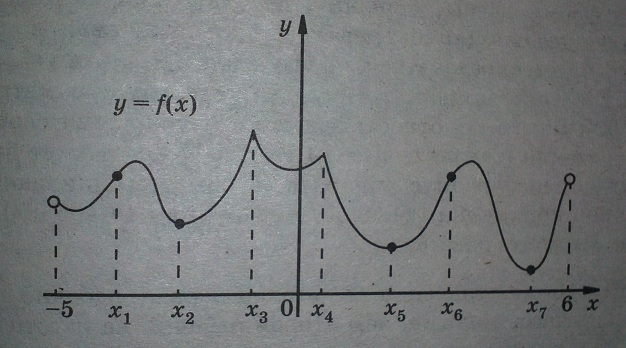
Решение:
Принцип в решении этой задачи такой: есть три возможных поведения функции на этом интервале:
1) когда функция возрастает (там производная больше нуля)
2) когда функция убывает (там производная меньше нуля)
3) когда функция не возрастает и не убывает (там производная либо равна нулю, либо не существует)
Нас интересует третий вариант.
Производная равна нулю где функция гладкая и не существует в точках излома. Рассмотрим все эти точки.
х1 - функция возрастает, значит производная f′(x) >0
х2 - функция принимает минимум и гладкая, значит производная f′(x) = 0
х3 - функция принимает максимум, но в этой точке излом, значит производная f′(x) не существует
х4 - функция принимает максимум, но в этой точке излом, значит производная f′(x) не существует
х5 - функция принимает минимум и гладкая, значит производная f′(x) = 0
х6 - функция возрастает, значит производная f′(x) >0
х7 - функция принимает минимум и гладкая, значит производная f′(x) = 0
Видим, что f′(x) = 0 в точках х2, х5 и х7, итого 3 точки.
Ответ: 3.

